Învățarea generalizată bazată pe mașini

Inteligența generală artificială are nevoie de un model mondial și de învățare automată generalizată, o abordare nouă a învățării automate.

Mașinile și paradigma lui Sisif

„Paradigma lui Sisif” se referă la un concept inspirat de figura mitologică greacă Sisif, care a fost condamnat să împingă veșnic un bolovan în sus doar pentru ca acesta să se rostogolească înapoi înainte de a ajunge în vârf. Paradigma lui Sisif este folosită metaforic pentru a descrie o situație sau o sarcină care este repetitivă, laborioasă și aparent fără sfârșit.

Într-un context mai larg, paradigma lui Sisif poate reprezenta orice activitate sau demers caracterizat de efort persistent și zadarnic. Este atunci când progresul este negat continuu de circumstanțe sau limitări inerente.

Paradigma lui Sisif sugerează un sentiment de luptă existențială, cu indivizi sau societăți prinși într-un ciclu de sarcini repetitive sau provocări care nu oferă nicio împlinire sau soluție durabilă.

Conceptul a fost aplicat în diferite domenii, inclusiv filozofie, literatură, psihologie și discuții despre existența umană. Este adesea invocat pentru a explora teme de lipsă de sens, condiția umană și natura perseverenței în fața adversității sau a obstacolelor aparent de netrecut.

9 din 10 manageri de active nu bat piața pe o perioadă de 10 ani. Dacă managerii nu o pot face, mașinile pot?

Mașinile amplifică părtinirile umane. Iar prejudecățile sunt complexe. Ele vin și pleacă, nu sunt permanente. Ele iau forme diferite și, în general,  nu sunt inteligibile pentru o persoană obișnuită.

Pentru a înțelege cum variabilitatea poate deveni nedetectabilă, ne putem uita la virusul SIDA care a rămas nedetectat deoarece are o variabilitate genetică ridicată. Cu alte cuvinte, și-a schimbat mereu forma.

Mașinile trebuie instruite pentru a înțelege părtinirile statistice, nu părtinirile umane înainte de a adopta o platformă meta-strategică.

Factori eronați

Toți factorii funcționează și eșuează temporar, iar dacă factorul Dimensiune ar putea fi un proxy, orice alt factor ar putea fi o funcție a ceva care se schimbă intrinsec, cum ar fi informațiile. Din punct de vedere istoric, societatea a încercat să se concentreze asupra unor astfel de factori eronați datorită confortului cauzalității și logicii intuitive. Refuzul de a accepta că corelația nu implică cauzalitate întărește părtinirea și amplifică eroarea.

Teoria prețurilor de arbitraj (APT) (Ross, 76) definește înlocuitori pentru a vinde la același preț folosind o măsurătoare de rentabilitate simplă. Dacă două active financiare oferă aceleași randamente financiare, acestea pot fi comparate. Ideea de înlocuire a lui Ross rămâne valabilă, însă factorul său sistematic rămâne incert. Ross spune că este determinat de factori neprevăzuți, deoarece ceea ce nu poți anticipa este ceea ce trebuie să gestionezi. Este un argument circular.

Pe de o parte, factorii sistematici nu pot fi anticipați. Cu toate acestea, pe de altă parte, sensibilitățile legate de acești factori pot ajuta administratorii de active și organizațiile în gestionarea fondurilor mari. Ross a definit sensibilitățile ca răspunsurile randamentelor activelor la mișcările neprevăzute ale factorilor economici.

„Dar care sunt acești factori?” Dacă i-am cunoaște, am putea măsura direct sensibilitățile stocurilor individuale față de fiecare. Din păcate, acest lucru este mult mai greu decât pare.

Pentru început, orice stoc este atât de influențat de forțele idiosincratice încât este foarte dificil să se determine relația precisă dintre randamentul său și un anumit factor. Cea mai mare problemă în măsurarea sensibilităților este separarea mișcărilor factorilor neprevăzuți de cei anticipați. Ar trebui să includem atât schimbările anticipate, cât și cele neprevăzute atunci când numai acestea din urmă sunt relevante… Indicele pieței nu trebuie ignorat, dar nici nu ar trebui să fie venerat. Este pur și simplu util ca reper la orizont…

Dovezile empirice recente au arătat fără echivoc că cei mai des utilizați indici de piață nu sunt portofoliile optimizate. În această condiție, CAPM beta nu este nici măcar un indicator de încredere al rentabilității așteptate și, așa cum am văzut deja, este practic inutilă ca măsură a tipului de risc la care este expus portofoliul…

Există mai mulți factori importanți și dacă toți nu sunt reprezentați, atunci înțelegerea noastră a modului în care funcționează piața de capital este inadecvată.

Ross subliniază necesitatea înțelegerii factorilor sistematici (inflația, producția industrială, primele de risc și ratele dobânzii). Deși subminează factorii idiosincratici, el totuși sugerează că „cumpărarea pieței” este pur și simplu greșită.

Deși APT și-a pierdut ușurința de utilizare în rândul utilizatorilor de-a lungul timpului, dezbaterea factorilor continuă până în prezent. Industria duce încă bătălia „factorul meu este mai bun decât factorul tău” în timp ce pierde războiul α. Mai mult, legea APT a prețului unic are o limitare temporală, deoarece piețele interacționează pe un continuum cu durate multiple.

Jacod și Yor (1977) au transformat „economia financiară” în „finanțare matematică”. Toate întrebările sunt puse în termeni pur matematici și nu apar principii economice fără o afirmație matematică precisă. Ipotezele APT sunt specifice domeniului, subiective și fără definiții matematice precise. Boussinesq (1897) l-a învățat pe Bachelier despre ecuațiile căldurii, pe care le-a combinat cu probabilitatea și cunoștințele burselor pentru a crea teoria matematică a speculației, piatra de temelie a finanțelor moderne așa cum o cunoaștem astăzi. Un sentiment de generalitate matematică se sustrage de la piață, deoarece se zvâcnește sub fluctuații speculative.

APT vs. CAPM vs. Modelul cu trei factori au performanțe care variază în funcție de perioada testată. Modelele sunt inconsecvente, contestate și preferate din cauza unor ipoteze sau preferințe de risc. Mențiunea fără echivoc a lui Fama că Size premium are performanțe slabe pentru perioade lungi este inexplicabilă. Investiția factorială nu este o știință. Eșecul factorilor este o realitate. Succesele factorilor sunt de scurtă durată și temporare. Forțele neprevăzute dincolo de factorii sistematici ai APT pot respinge și accepta un factor. Primele de risc pot fi explicate probabilistic. Explicațiile cauzale ale primelor de risc se adaugă la ineficiența pieței. Fama își construiește cazul provocând SLB. În timp ce finanțarea comportamentală își construiește cazul factorului (psihologia) provocând EMH. Prescott (2008) a scris că „Raj și cu mine am ajuns la concluzia că prima de acțiuni trebuie să fie pentru altceva… descoperirea noastră a fost că riscul nediversificabil a reprezentat doar o mică parte din diferența dintre randamentele medii istorice”.

Generarea semnificației statistice este ușoară. 200 până la 300 de variabile generează de obicei doi până la trei factori semnificativi statistic, chiar dacă nu există o relație de bază reală. Deci, cu cât mai multe variabile într-un model, cu atât este mai probabilă șansa ca câteva variabile să evoce sens, atunci când acesta nu există. (Investiții alternative, abordarea unui alocător, Chambers, Kazemi, Black, Wiley 2021)

Timing Campbell, Goodhart și Factor

Un statistician instruit în istorie economică și cicluri economice va indica fără efort legea eșecului a lui Campbell și Goodhart (C&G). El va reitera, de asemenea, că ciclurile sunt ca niște indicatori, menite să eșueze. Confirmarea unui model nu elimină probabilitatea de eșec al acestuia. Indiferent de semnificația pe care o acordăm variabilelor noastre, ele sunt menite să ne dezamăgească, să stagneze și, în cele din urmă, să devină inutile. Eșecul indicator și variabil este realitate. Și există o variabilă care nu va dispărea niciodată: zgomotul, haosul, turbulența, incertitudinea etc. Prin urmare, analiza importanței caracteristicilor este ca povestea orbilor și a elefanților. Elefantul poate fi găsit doar dacă orbii se ocupă de ceea ce este inobservabil și inexplicabil.

Acesta este motivul pentru care atunci când găsiți funcții importante și efectuați experimente, ar trebui să știți că în cele din urmă aceste caracteristici nu vor mai funcționa în anumite medii specifice. După aceea, unele regimuri se vor schimba și importanța caracteristicilor se va diminua și mai mult în timp. Semnalarea predictibilității și aplicabilității va influența negativ caracteristicile din alte clase de active. Și în cele din urmă, o caracteristică importantă care a început ca un instrument de cercetare va arăta ca un ciclu de backtest eșuat. În momentul în care îl introduci în aplicație, nu mai funcționează. Acesta este motivul pentru care știința se confruntă cu o criză de replicabilitate. Rezultatele sunt valabile până când le publicați ca lucrare de cercetare. Dar odată ce rezultatele sunt articulate, comportamentul se schimbă. Cercetarea este inutilă.

În mod similar, randamentele activelor nu sunt distribuite în mod normal, dar în momentul în care le puneți pentru a testa o criză de impuls distruge persistența. Ideea de fluctuație imprevizibilă este, așa cum sugerează și numele, imprevizibilă. Și chiar dacă presupunem că un indicator nu este înșelat de C&G, sincronizarea factorilor este imposibilă. Răspândirea va diverge mai mult decât perioada în care sunteți solvent. Sistemul este echipat pentru o anticipare consecventă. Timpul este imposibil.

Factorul generalizat

Variabilele observabile și explicabile joacă un rol crucial în înțelegerea sistemelor complexe. Cu toate acestea, este imperativ să recunoaștem că nu toate variabilele se încadrează perfect în aceste categorii. Există întotdeauna șansa ca o variabilă să nu fie nici observabilă, nici ușor explicabilă, introducând incertitudine și zgomot în ecuație. Acest zgomot complică anticiparea și predicția. Ne reamintește că, chiar și cu date extinse și modele explicative, viitorul rămâne incert. Îmbrățișarea acestei incertitudini necesită umilință, adaptabilitate și dorința de a ne actualiza înțelegerea pe măsură ce apar informații actualizate. Navigarea în complexitatea variabilelor imprevizibile este o provocare continuă în multe domenii, care necesită vigilență constantă și o abordare nuanțată a procesului decizional.

În contextul observabilității, explicabilității și eșecului, modelarea zgomotului sau absența acestuia necesită înțelegerea incertitudinilor inerente în sistem. Zgomotul se referă la fluctuații aleatorii sau variații inexplicabile ale datelor, în timp ce semnalul reprezintă informațiile semnificative pe care ne propunem să le extragem.

Pentru a modela zgomotul, pot fi folosite tehnici statistice. Aceste tehnici analizează modele, tendințe și corelații în date pentru a identifica semnalele de bază. Cu toate acestea, este esențial să recunoaștem că, chiar și cu modele sofisticate, semnalul estimat nu este niciodată absolut. Este în mod inerent probabilistic, oferind mai degrabă o serie de rezultate posibile decât un răspuns definitiv.

Când timpul este adăugat ca o variabilă la model, estimarea probabilistică a semnalului se poate modifica. Acest lucru se datorează faptului că sistemul poate evolua, noi date pot deveni disponibile sau înțelegerea noastră a factorilor de bază se poate îmbunătăți în timp. Ca rezultat, probabilitățile estimate asociate cu diferite rezultate se pot schimba pe măsură ce culegem mai multe informații.

Pentru un cititor neprofesionist, gândiți-vă astfel: Imaginează-ți că încerci să prezici vremea pentru săptămâna viitoare. Ai date istorice, modele de prognoză și cunoștințe meteorologice care să te ghideze. Cu toate acestea, din cauza complexității modelelor meteorologice și a incertitudinilor inerente implicate, predicția ta nu este o garanție a ceea ce se va întâmpla. Este o estimare bazată pe informațiile disponibile și, pe măsură ce timpul trece și noi date devin disponibile, estimarea ta se poate modifica. Același lucru este valabil și pentru alte domenii în care incertitudinile și variabilele intră în joc. Modelele probabilistice ne ajută să facem judecăți în cunoștință de cauză, recunoscând în același timp limitările de certitudine absolută.

Prin urmare, un factor generalizat, să-l numim „factorul X”, (f) poate fluctua între a fi relevant și irelevant, aplicabil și redundant, anticipat și duce la eșec. Ne putem gândi la acest factor X ca la un lanț Markov idealizat.

Lanțul Markov este un model matematic care reprezintă un sistem. Este locul în care starea viitoare a sistemului depinde doar de starea sa actuală și nu de modul în care a ajuns la acea stare. În cazul nostru, factorul X poate fi în diferite stări (de exemplu, relevant sau irelevant) și poate trece între aceste stări pe baza anumitor probabilități.

De exemplu, factorul X poate fi relevant și aplicabil într-o situație, dar pe măsură ce circumstanțele se schimbă, poate deveni redundant sau irelevant. În mod similar, putem anticipa că factorul X are un anumit impact. Cu toate acestea, din cauza unor factori neprevăzuți sau a condițiilor în schimbare, poate duce la eșec sau poate avea un rezultat diferit de cel așteptat.

Este important că aceste tranziții în relevanța, aplicabilitatea, anticiparea sau eșecul factorului X pot fi, de asemenea, influențate de timp. Pe măsură ce timpul trece, factorul X poate evolua sau își poate schimba starea. Schimbarea informațiilor, evenimentelor sau condițiilor poate afecta relevanța sau aplicabilitatea acestora, ducând la rezultate diferite pe măsură ce trece timpul. [N] este starea normală, în timp ce [NN] este starea nenormală.

În esență, a vedea factorul generalizat ca pe un lanț Markov idealizat înseamnă să recunoaștem că se poate schimba dinamic între stări. Aceste tranziții pot fi influențate de timp și de diverși factori. Această înțelegere evidențiază complexitatea și incertitudinea factorului X. Ea subliniază necesitatea unor abordări adaptabile și flexibile atunci când se confruntă cu astfel de variabile. Factorul X poate fi văzut și ca un factor compozit, multiplu la lucru.

Când privim factorii ca sisteme dinamice, aceștia pot prezenta diverse stări sau condiții în timp. În loc să fie fixat într-o singură stare, un factor poate exista probabil în mai multe stări simultan.

Pentru a ilustra acest lucru, imaginează-ți un factor numit „A” care are două stări: starea 1 și starea 2. În loc să fie exclusiv într-o stare sau alta, factorul A poate avea o anumită probabilitate de a fi în starea 1 și o altă probabilitate de a fi în starea 2 la un moment dat. Aceste probabilități reprezintă probabilitatea sau șansa ca factorul să fie observat în fiecare stare.

Deoarece un factor poate fi în mai multe stări simultan, probabilitatea totală pentru toate stările posibile trebuie să însumeze 1. Cu alte cuvinte, probabilitatea globală a sistemului este întotdeauna 1 deoarece cuprinde toate stările potențiale pe care le poate ocupa factorul. Acest principiu este valabil datorită naturii închise a sistemului, ceea ce înseamnă că toate stările posibile sunt contabilizate în limitele sistemului.

Considerând factorii ca sisteme dinamice și înțelegerea naturii probabilistice a acestora, putem lua în considerare incertitudinile inerente și variabilitatea sistemului. Această perspectivă ne permite să surprindem complexitatea factorilor și capacitatea lor de a exista în mai multe stări simultan. De asemenea, asigură că probabilitatea totală a sistemului rămâne constantă și cuprinzătoare. Acest factor generalizat poate exprima multe distribuții statistice, dar nu în același timp.

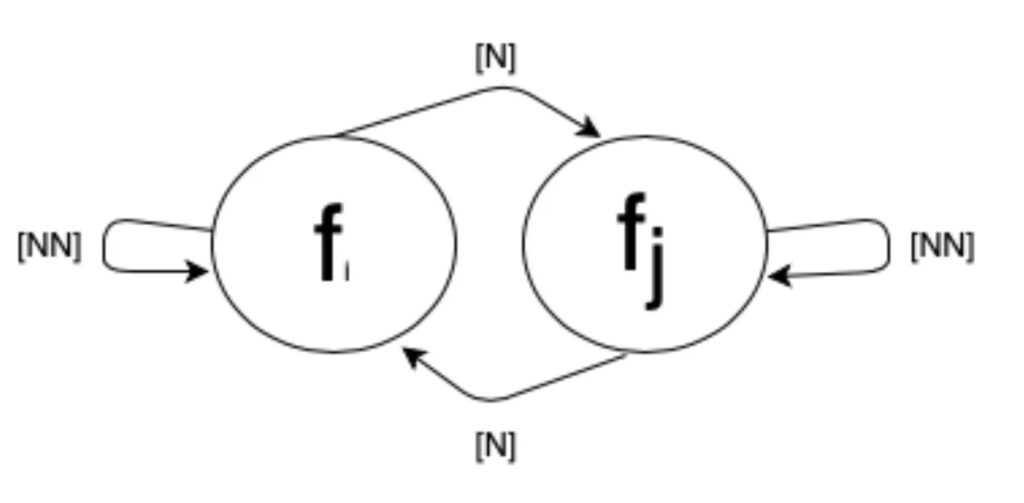
Stări probabilistice

Deoarece distribuțiile statistice pot fi clasificate la granițele dintre normal și non-normal, acest sistem probabilistic a exprimat atât caracteristicile reversiunii medii, cât și eșecul reversiunii medii care a condus la extremități, cozi grase, adică un comportament nenormal.

Conceptele de inversare medie și eșecul reversiunii medii sunt relevante atunci când se ia în considerare comportamentul de distribuție statistică și relația lor cu extremitățile și cozile grase.

Reversia medie se referă la tendința unei variabile sau a unui sistem de a se întoarce spre media sausă fie medie în timp. Cu alte cuvinte, atunci când o variabilă se abate semnificativ de la medie, se așteaptă ca în cele din urmă să revină la valoarea medie.

Cu toate acestea, în unele cazuri, inversarea medie poate eșua sau poate fi incompletă. Acest lucru poate apărea din cauza diferiților factori, cum ar fi schimbări structurale, evenimente extreme sau tendințe persistente. Când revenirea la medie eșuează, poate duce la comportamente care se abat de la așteptările normale ale distribuției.

O consecință a eșecului reversiunii medii este apariția extremităților sau a valorii aberante. Acestea sunt observații care se încadrează în cozile distribuției și sunt departe de medie. Într-o distribuție normală, cozile sunt relativ subțiri, ceea ce indică faptul că este mai puțin probabil să apară valori extreme. Cu toate acestea, atunci când reversiunea medie eșuează, evenimentele sau valorile extreme pot deveni mai frecvente, rezultând cozi grase în distribuție.

Cozile grase se referă la o distribuție care are mai multe observații în cozi decât se aștepta într-o distribuție normală. Aceasta indică o probabilitate mai mare de valori sau evenimente extreme decât predicțiile de distribuție normală. Cozile grase sunt adesea asociate cu un comportament nenormal și pot avea implicații pentru managementul riscurilor, deoarece implică o probabilitate mai mare de rezultate extreme decât o distribuție normală.

Eșecul reversiunii medii poate duce la un comportament nenormal în distribuțiile statistice, inclusiv apariția extremităților și a cozilor grase. Aceste fenomene evidențiază necesitatea de a lua în considerare și de a lua în considerare evenimentele extreme și comportamentul nenormal atunci când se analizează și se modelează datele din lumea reală.

Termenii „bogatul-devine-mai-bogat” și „săracul-devine-mai sărac” descriu anumite dinamici în cadrul unui sistem, în special despre distribuția resurselor sau a bogăției. Această dinamică poate duce la un comportament nenormal în cadrul unor distribuții specifice. Cu toate acestea, merită să reții că normalitatea sau non-normalitatea este o proprietate statistică a distribuției ca întreg, mai degrabă decât o proprietate inerentă a stărilor sau fenomenelor individuale din distribuție.

În termeni statistici, normalitatea se referă la o distribuție matematică specifică numită distribuție normală sau distribuție Gaussiană. Se caracterizează printr-o curbă simetrică în formă de clopot. Comportamentul nenormal se referă la abaterile de la acest model în formă de clopot.

Fenomenele ”bogații-se îmbogățesc” și ”săracii-devin-mai săraci”pot duce la abateri de la o distribuție normală. Ele pot provoca distribuții ale legii puterii, în cazul în care un număr mic de indivizi sau entități de mare succes dețin o cantitate disproporționată de resurse sau bogăție. Aceste distribuții ale legii puterii sunt caracterizate de cozi lungi, indicând o probabilitate mai mare de evenimente sau valori extreme.

Prin urmare, putem spune că dinamica bogatul-devine-mai-bogat și săracul-devine-mai sărac sunt asociate cu stări non-normale în cadrul unei distribuții. Aceste stări non-normale se manifestă ca valori sau evenimente extreme la capătul de coadă a distribuției. Cu toate acestea, este esențial să ne amintim că distribuția generală în sine poate prezenta în continuare caracteristici de normalitate sau non-normalitate, în funcție de forma și proprietățile statistice în ansamblu.

În rezumat, fenomenele bogatul-devine-mai-bogat și săracul-devine-mai sărac pot contribui la un comportament nenormal în cadrul unor distribuții specifice, caracterizate prin distribuții ale legii puterii cu cozi lungi. Cu toate acestea, normalitatea sau non-normalitatea este o proprietate statistică a întregii distribuții, iar stările sau fenomenele individuale din cadrul distribuției pot prezenta un comportament nenormal fără a defini neapărat întreaga distribuție ca nenormală.

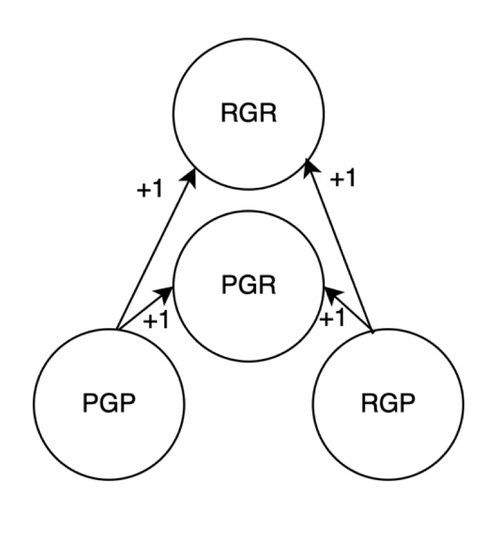
Risc idealizat

Acum imaginează-ți acest factor dinamic pe o piață idealizată. Sunt două forțe opuse în joc. Pe de o parte, există forța de întoarcere, care tinde să tragă lucrurile înapoi spre o stare echilibrată. Pe de altă parte, există forța de diversiune, care face ca lucrurile să se abată de la acea stare echilibrată.

În acest scenariu idealizat, atât inversarea, cât și diversiunea au putere egală, ceea ce înseamnă că trag în mod egal din ambele părți. Acest lucru creează o situație în care piața este în flux constant, mișcându-se între stările de convergență și divergență.

Riscul apare din imprevizibilitatea comportamentului pieței din cauza acestor forțe opuse. Deoarece reversiunea și deturnarea sunt ambele influente, devine dificil să anticipăm direcția pieței cu certitudine.

Fluctuațiile pieței introduc incertitudine și fac dificilă realizarea de predicții precise. Ca rezultat, investitorii și participanții la piață se confruntă cu un risc crescut, deoarece nu se pot baza pe un model sau o tendință simplă. Echilibrul dintre revenire și diversiune creează un element de imprevizibilitate care se adaugă la factorul de risc.

Într-un astfel de scenariu, investitorii trebuie să analizeze cu atenție piața și să adopte o perspectivă pe termen lung.

Înțelegând interacțiunea dintre revenire și deturnare, investitorii își pot gestiona riscul prin diversificarea investițiilor. Ei pot adopta, de asemenea, o abordare răbdătoare care ține cont de incertitudinile inerente ale factorilor dinamici.

În acest scenariu idealizat, inversarea este forța care trage lucrurile înapoi către o stare echilibrată, în timp ce devierea este forța care provoacă abateri de la acea stare echilibrată, creând dezechilibru și, prin urmare, o stare perpetuă de mișcare.

Acum, să luăm în considerare valorile asociate cu această stare idealizată. Factorul RD reprezintă interacțiunea dintre inversare (R) și diversiune (D) și distribuie o probabilitate uniformă în patru subfactori. Beta, care este însumarea tuturor subfactorilor, măsoară riscul general de piață sau expunerea.

În acest cadru, putem ilustra conceptul de Alpha și Smart Beta. Alfa (⍶) reprezintă selecția pozitivă sau depășirea performanței și este combinația dintre fenomenele de îmbogățire bogată (RGR) și fenomene de îmbogățire săracă (PGR).

Pe de altă parte, Alpha Prime (⍶’) este inversul Alpha și constă din setul tuturor selecțiilor slabe sau performanțelor slabe. Este cunoscut și sub numele de Dumb Beta.

În această stare idealizată, riscul provine din natura dinamică a factorului RD și din interacțiunea dintre reversiune și diversiune. Echilibrul dintre aceste forțe creează fluctuații constante pe piață, ceea ce face dificilă prezicerea cu precizie a direcției acesteia.

Această imprevizibilitate crește riscul pentru investitori și participanții la piață. Comportamentul pieței este influențat atât de selecția pozitivă (Smart Beta), cât și de selecția negativă (Dumb Beta), care pot varia în timp.

Încasări în exces

(Alfa) există datorită fluctuațiilor dinamice. Cu toate acestea, riscul constă în prezicerea cu exactitate a probabilităților Smart Beta și Dumb Beta.

Investitorii trebuie să fie conștienți de acest risc și să abordeze piața pe termen lung. Diversificându-și investițiile și adoptând o abordare răbdătoare și pasivă, investitorii pot minimiza probabilitatea de a fi afectați negativ de Dumb Beta. În plus, pot maximiza probabilitatea de a obține beneficii Smart Beta.

Pe scurt, riscul în această stare idealizată provine din natura dinamică a factorului RD. De asemenea, apare din interacțiunea dintre reversiune și diversiune și imprevizibilitatea pe care o introduce. Înțelegerea acestor dinamici și adoptarea unei abordări de investiții pasive pe termen lung poate ajuta la gestionarea riscurilor.

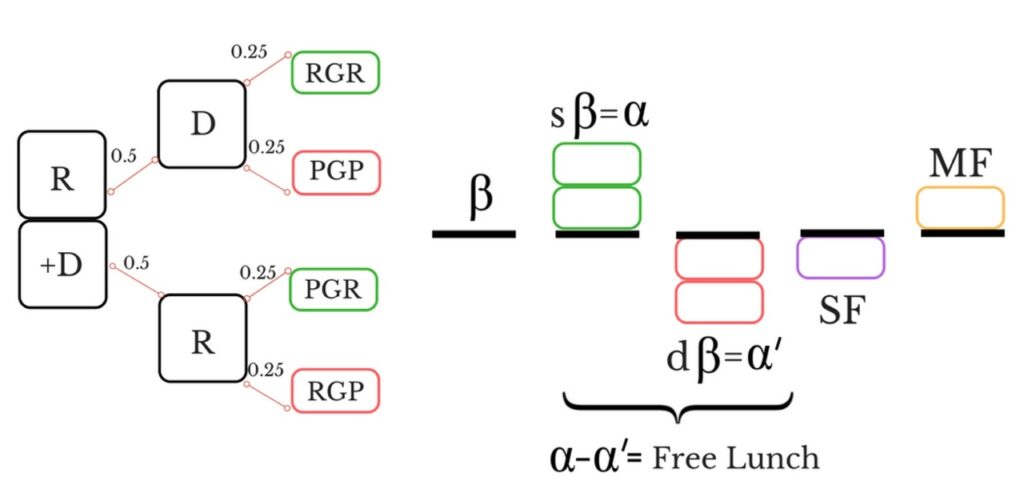
Lanțurile Markov ca sistem dinamic

Un lanț Markov poate fi într-adevăr ilustrat ca un sistem dinamic. Lanțul Markov este un model matematic care descrie o succesiune de evenimente sau stări. În acest model, probabilitatea trecerii de la o stare la alta depinde doar de starea actuală și nu de istoria trecută. Poate fi reprezentat ca un grafic direcționat, unde stările sunt reprezentate prin noduri, iar tranzițiile dintre stări sunt reprezentate prin muchii direcționate.

Când ilustrăm un lanț Markov ca un sistem dinamic, putem vizualiza tranzițiile între stări în timp. Pornind de la o stare inițială, sistemul trece de la o stare la alta pe baza probabilităților de tranziție. Această mișcare între stări poate fi reprezentată printr-o succesiune de instantanee sau animații. Aceasta arată progresul sistemului prin diferite stări pe măsură ce trece timpul.

Reprezentând lanțul Markov ca un sistem dinamic, putem obține informații despre comportamentul și evoluția sistemului în timp. Putem analiza proprietăți precum convergența către echilibru, modelele recurente sau comportamentul pe termen lung. Vizualizarea dinamicii unui lanț Markov ne poate îmbunătăți înțelegerea naturii probabilistice. De asemenea, poate oferi o reprezentare vizuală a modului în care sistemul evoluează prin diferite stări în timp.

Staționaritate, memorie și mecanisme neliniare

Da, este în general adevărat că stabilirea datelor staționare poate elimina sau reduce efectiv dependențele de memorie sau temporale. Staționaritatea se referă la o proprietate a datelor în care proprietățile statistice, cum ar fi media și varianța, rămân constante în timp sau în diferite subseturi de date.

Când datele prezintă non-staționaritate, înseamnă că proprietățile statistice ale datelor se modifică în timp și pot exista dependențe sau tendințe temporale prezente. În astfel de cazuri, datele pot prezenta memorie, ceea ce înseamnă că valoarea curentă a unui punct de date poate fi influențată de valorile sale trecute.

Prin transformarea datelor non-staționare în date staționare, elimini modelele și dependențele dependente de timp. Acest lucru poate fi atins prin tehnici precum eliminarea tendințelor, diferențierea sau transformarea datelor folosind operații matematice. Scopul este de a elimina tendințele, sezonalitatea sau alte modele care variază în timp, făcând datele staționare.

Odată ce datele sunt staționate, proprietățile statistice devin constante în timp și orice dependențe de memorie sau temporale sunt eliminate sau reduse semnificativ. Acest lucru este adesea de dorit în modelarea și analiza statistică, deoarece simplifică datele și permite aplicarea diferitelor tehnici de modelare care presupun staționare.

Cu toate acestea, este important de reținut că procesul de staționare a datelor și de eliminare a memoriei nu este întotdeauna adecvat sau necesar pentru toate tipurile de analiză a datelor. În unele cazuri, păstrarea dependențelor temporale sau a memoriei în date este esențială pentru modelarea și analiza precisă. Decizia de a staționa datele sau de a păstra memoria depinde de contextul și obiectivele specifice ale analizei.

Datele staționare, prin definiție, nu ar trebui să aibă modele sau tendințe dependente de timp. Cu toate acestea, pot exista scenarii în care datele par staționare, dar păstrează în continuare dependențe de memorie sau temporale. Acest lucru se poate întâmpla în următoarele condiții:

1. În ciuda faptului că sunt staționare, datele pot avea în continuare memorie dacă prezintă modele sau cicluri repetate. De exemplu, în datele seriilor de timp sezoniere, observațiile pot arăta fluctuații regulate pe anumite intervale de timp, indicând memoria sezonieră.
2. Procese autoregresive: Chiar și datele staționare pot prezenta memorie datorită proceselor autoregresive. Modelele autoregresive încorporează valori întârziate ale variabilei în sine ca predictori, care introduc dependențe de memorie sau temporale. Aceste modele surprind relația dintre valorile actuale și trecute și pot păstra memorie chiar și în datele staționare.
3. Dependențe pe termen lung: Anumite tipuri de date pot avea dependențe pe termen lung, unde observațiile din trecut influențează valorile imediate sau din apropiere. Aceste dependențe pot persista chiar și în datele staționare, indicând memoria pe scale de timp mai lungi.
4. Dependențe neliniare: staționaritatea presupune proprietăți statistice constante în timp. Cu toate acestea, dacă datele prezintă dependențe neliniare, cum ar fi interacțiuni complexe sau mecanisme de feedback, memoria poate fi prezentă chiar și în datele staționare.

În aceste condiții, deși datele pot fi considerate staționare pe baza proprietăților statistice precum media și varianța, există încă modele subiacente, cicluri, procese autoregresive sau dependențe pe termen lung care introduc dependențe de memorie sau temporale.

Universalitate și generalizare

„Universal” în contextul unui mecanism implică de obicei capacitatea acestuia de a se generaliza în diferite domenii, contexte sau surse de date. Un mecanism universal surprinde tiparele și relațiile de bază care sunt valabile în diverse setări. Acest lucru îi permite să-și aplice cunoștințele și cunoștințele la date noi și nevăzute.

Generalizarea se referă la capacitatea unui model sau mecanism de a funcționa bine pe date pe care nu a fost instruit direct. Înseamnă că cunoștințele și modelele învățate din datele de antrenament pot fi aplicate eficient pentru a face predicții sau decizii precise cu privire la punctele de date nevăzute sau viitoare.

Învățarea automată necesită generalizare. Se asigură că modelul sau mecanismul poate gestiona noi instanțe de date sau scenarii dincolo de datele de antrenament, făcându-l aplicabil în setările din lumea reală.

Un mecanism universal, care își poate generaliza cunoștințele învățate în diferite domenii, clase de active, regiuni sau instrumente, își propune să capteze și să valorifice principii sau modele fundamentale care sunt aplicabile pe scară largă. Această universalitate permite mecanismului să se adapteze și să funcționeze bine în contexte diverse, chiar și fără o cantitate mare de date specifice de antrenament în fiecare context.

Cu toate acestea, este esențial să reții că, în timp ce un mecanism universal poate avea potențialul de generalizare, succesul real al generalizării depinde de diverși factori. Acești factori includ calitatea și diversitatea datelor de instruire, complexitatea problemei și eficacitatea algoritmilor de învățare utilizați.

Backdating vs. Backtesting

Universalitatea, în contextul diferențierii între backdating și backtesting, se poate referi la capacitatea unui mecanism de a capta și de a se adapta la date dinamice și la condițiile pieței.

Datarea anterioară se referă la practica de a atribui date sau informații istorice la un anumit moment în timp. Aceasta este pentru a simula performanța sau comportamentul unui mecanism sau strategie. Aceasta implică aplicarea retroactivă a unui mecanism datelor anterioare pentru a evalua eficiența potențială a acestuia.

Backtesting-ul, pe de altă parte, implică testarea unui mecanism sau strategie pe date istorice pentru a-i evalua performanța. De asemenea, face proiecții despre comportamentul său viitor. Aceasta implică simularea tranzacțiilor, a alocărilor de portofoliu sau a proceselor de luare a deciziilor pe baza datelor istorice pentru a evalua rentabilitatea potențială sau riscul asociat mecanismului.

Universalitatea poate ajuta la diferențierea între backdating și backtesting, deoarece un mecanism universal se adaptează și se generalizează în diferite surse și perioade de date. Poate face față în mod eficient naturii dinamice a datelor și a condițiilor de piață, permițând testări și proiecții mai precise în viitor.

Prin încorporarea principiilor și modelelor universale care se aplică în diferite domenii și perioade, un mecanism universal poate oferi informații și predicții mai fiabile în timpul testării backtesting. Se poate adapta la dinamica pieței în schimbare și poate capta factorii esențiali care stimulează performanța, permițând o evaluare mai realistă a potențialei sale eficiențe.

În schimb, un mecanism care nu are universalitate poate avea dificultăți să se adapteze la date noi sau nevăzute, ceea ce duce la rezultate nesigure de backtesting. Este posibil să nu capteze modele critice sau să țină seama de schimbările condițiilor pieței, ceea ce duce la proiecții inexacte și la concluzii înșelătoare.

Prin urmare, universalitatea unui mecanism poate juca un rol semnificativ în diferențierea dintre backdating și backtesting, asigurându-se că mașina poate captura și se poate adapta în mod eficient la natura dinamică a datelor și a condițiilor de piață, conducând la evaluări mai precise și mai fiabile ale performanței sale.

Un proces universal ar fi, prin urmare, ușor din punct de vedere computațional și ar obține rezultate mai mari fără a se baza pe prea multe date. Acest lucru va evita alte provocări legate de date, cum ar fi supraadaptarea testului de bază, scurgerile de validare încrucișată, etichetarea unui orizont de timp fix etc.

Învățarea automată generalizată

Un factor generalizat este bazat pe o clasare staționară, care funcționează ca lanțuri Markov, cu probabilitățile ca acești factori să atingă un stadiu de echilibru. Aceasta pune bazele unui proces generalizat de învățare automată care face următoarele.

1. Clasifică datele: Aduni date care reprezintă clasarea staționară a factorilor în timp. O analiză a datelor ar trebui să reflecte ordinea relativă sau importanța factorilor și evoluția lor în timp.
2. Reprezentare staționară de clasare: Definești și reprezinți stările de clasare staționare ale factorilor. Fiecare stat reprezintă o ordine sau un aranjament specific de factori în funcție de importanța lor.
3. Estimarea matricei de tranziție: Estimezi probabilitățile de tranziție între stările de clasare staționare pe baza datelor observate. Analizezi frecvența tranzițiilor și calculezi probabilitățile. În acest caz, probabilitățile de tranziție ar reprezenta probabilitatea unor modificări în importanța relativă a factorilor.
4. Modelul lanțului Markov: utilizezi un model al lanțului Markov pentru a captura comportamentul staționar al factorilor. Stările modelului reprezintă diferitele clasamente staționare, iar probabilitățile de tranziție reflectă probabilitățile de tranziție între clasamente.
5. Antrenament și deducere: Antrenezi modelul în lanțul Markov folosind date de clasare pentru a estima parametrii modelului, inclusiv probabilitățile de tranziție. Odată antrenat, modelul poate deduce și prezice cea mai probabilă secvență de clasamente staționare având în vedere datele observate.
6. Validarea modelului: Evaluezi performanța modelului în lanțul Markov folosind metrici de evaluare adecvate, cum ar fi log-probabilitatea sau perplexitatea. Asigură-te că modelul surprinde cu acuratețe comportamentul de clasare staționar și prezice importanța relativă a factorilor.
7. Implementarea modelului: implementezi modelul în lanț Markov pentru a prezice date actualizate. Monitorizezi performanța modelului și verifici dacă acesta continuă să se alinieze cu comportamentul de clasare staționar observat.

Atunci când factorii se bazează pe o clasare staționară și pot fi modelați ca lanțuri Markov cu probabilități de echilibru, procesul generalizat de învățare automată se concentrează pe captarea și modelarea tranzițiilor între stările de clasare staționare. Modelul Markov în lanț oferă informații despre importanța relativă a factorilor și permite predicții bazate pe clasamente staționare.

Concluzie

Învățarea generalizată bazată pe mașini se bazează pe factori generalizați care funcționează ca parte a mecanismului, prezintă universalitate, sunt date și calcule ușoare și pot răspunde la o gamă largă de întrebări problematice în comparație cu domeniul limitat de factori convenționali determinati de părtinirea umană.

Acest articol este scris de Mukul Pal, lector AS Financial Markets și antreprenor de succes cu o experiență de peste 20 de ani în investiții. Mukul Pal prezintă programul Machine Investing, un curs deosebit de util, care educă investitorul despre utilitatea informațiilor financiare în construirea unui portofoliu de investiții. Pentru înscrieri și detalii, ne poți contacta la office@cursuribura.ro sau la numărul de telefon: +40-771.261.036.

Articolul poate fi citit în original, în limba engleză aici.  

Citește și: Valoarea are performanțe slabe!